Homing Missile Tutorial - Game Maker Studio 2
This tutorial will show you how to program a homing missile to follow the main player in Game Maker Studio 2 (GMS2). The programming syntax will be for GMS2, but the logic can be applied to any game engine!
STEP 1: PSEUDO CODE AND ART
Before we start making any art or programming, let’s write out some pseudo code so we can properly understand what we need to code.
Get the vector angle between the homing missile and the main player
Based on that angle, the head of the homing missile needs to turn towards the main player
Wow, that sounds easy! Right?! =S
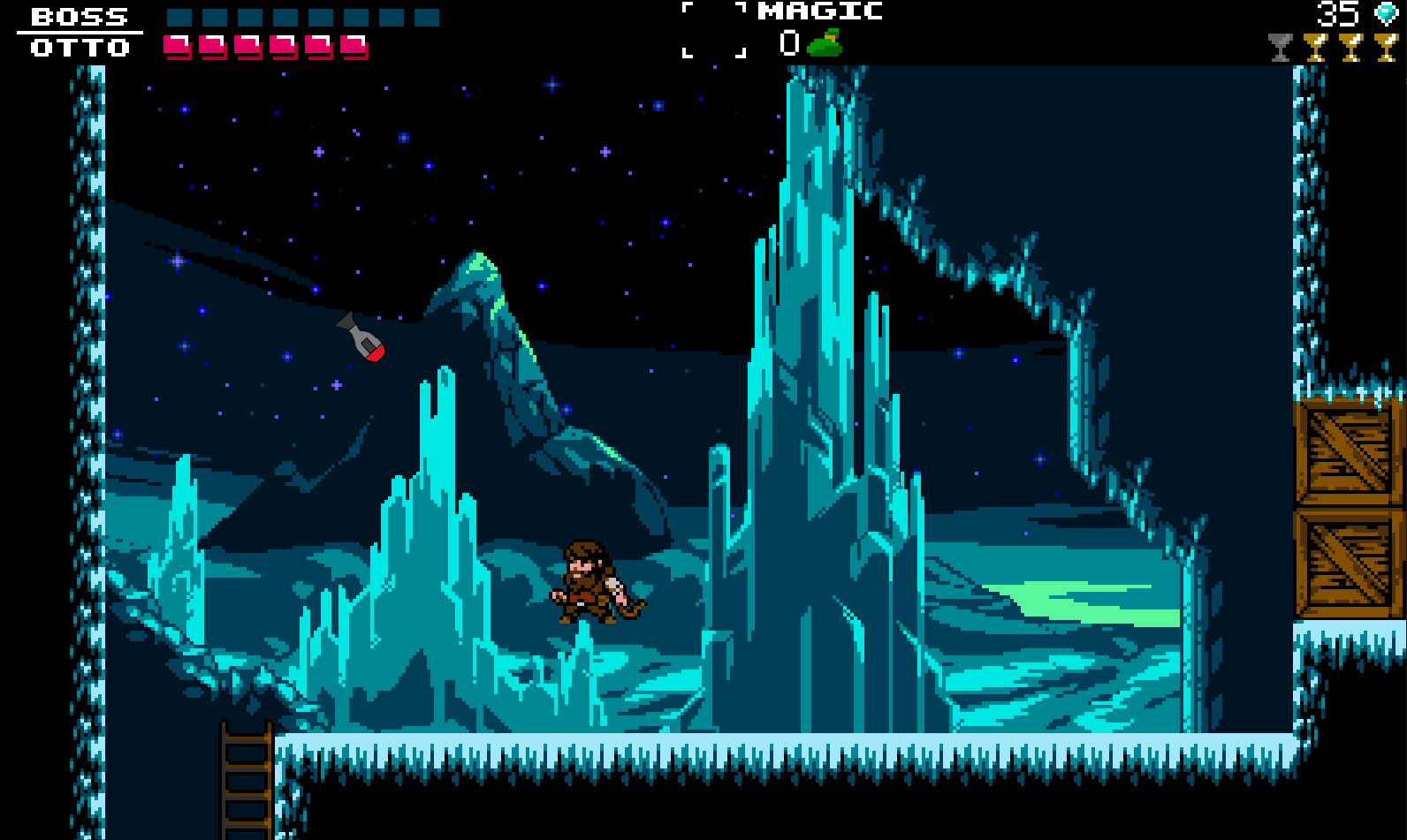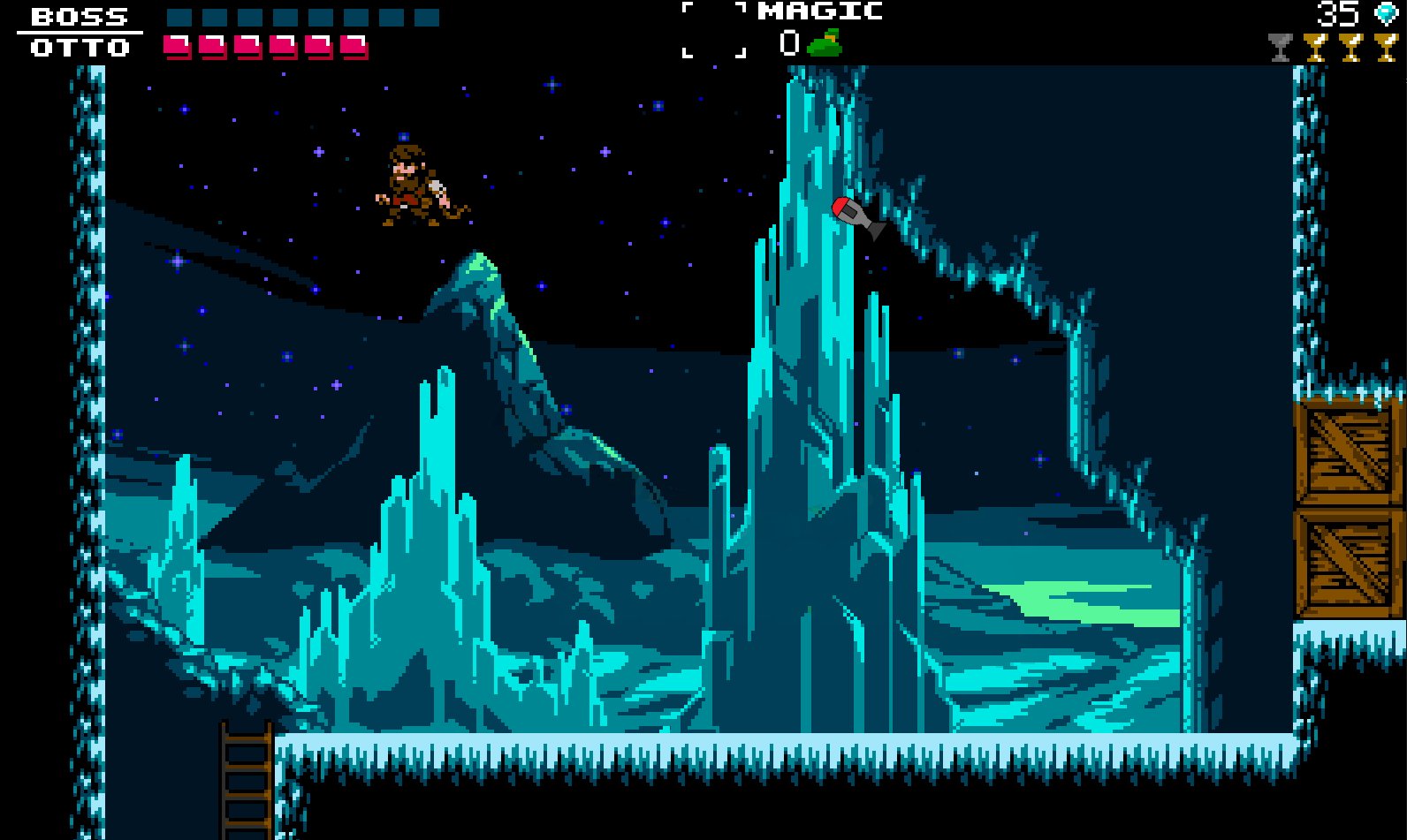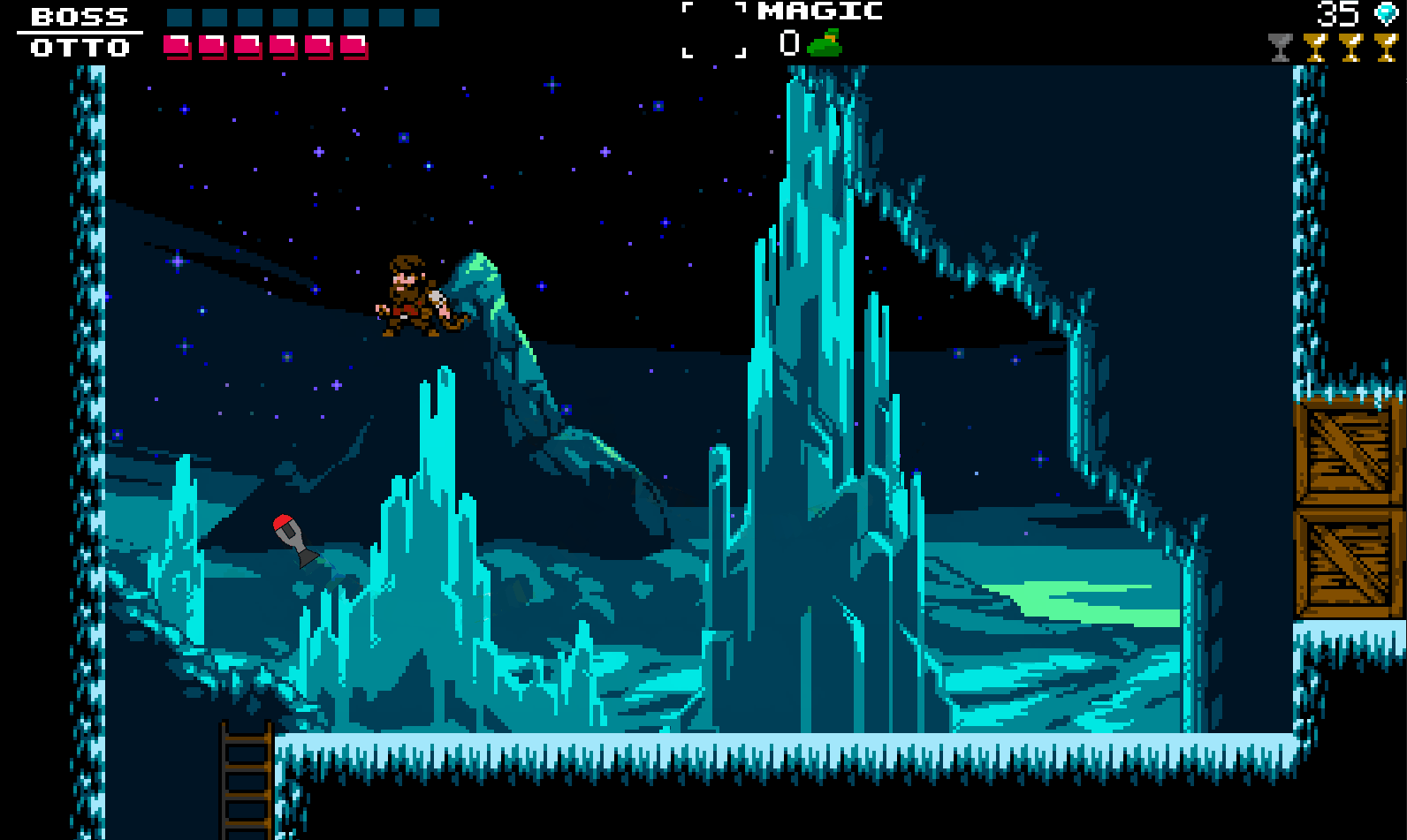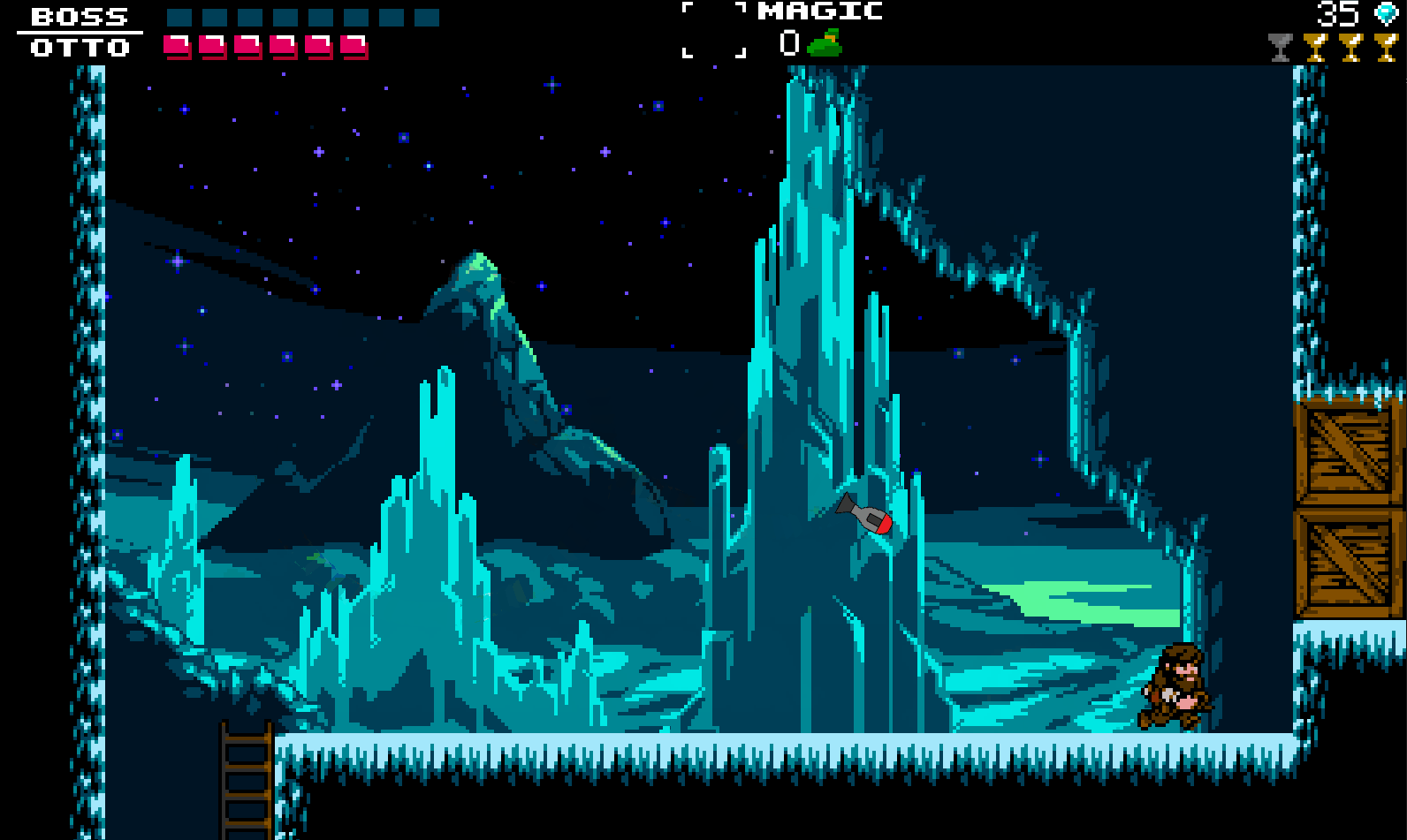
Now we need art for the homing missile. Below you’ll see the homing missile which I made (feel free to use my image, I am the BEST artist lol). Keep in mind, that you want the missile to be pointing to the right just like my image is. Therefore the homing missile at 0 degrees points right, at 90 degrees points up, 180 degrees points to the left, and 270 degrees points down.
And for the main player, we will be using Otto from our own game!
STEP 2: PROGRAMMING
At this point we will assume there is already a GMS2 Object for the main player called obj_main_player. Now let’s create a new Object in GMS2 and name it obj_homing_missile. This homing missile object will need 2 events, Create and Step. If you haven’t used GMS2 before - Create is called when an instance of the object is first created, and Step is the Update function.
Below is the obj_homing_missile Create event:
// Target the homing missile follows
target = obj_main_player;
// Velocity of homing missile
velocity = 5;
// Turning direction speed of homing missile
turnSpeed = 1.5;
// Stores vector angle between homing missile and main player
pointDifference = 0;
// Stores value which determines direction homing missile will turn to target
angleDirection = 0;
Above you will see the variable target which is the object that the homing missile will follow. Here we set it to the main player. The variable velocity is the velocity of the homing missile, and turnSpeed will be how quick the homing missile can change its angle. The variable pointDifference will store the vector angle between the homing missile and the main player. This variable will become more clear in the Step event. Finally the variable angleDirection will be used to determine which direction the homing missile should turn to face the main player.
Below is the obj_homing_missile Step event:
// Vector angle between homing missile and target
pointDifference = point_direction(x, y, target.x, target.y);
// Sin in degrees of vector angle minus current direction
angleDirection = dsin(pointDifference - direction);
// Determine which direction to turn and set direction
if(angleDirection > 0)
{
direction = direction + turnSpeed;
}
else if(angleDirection < 0)
{
direction = direction - turnSpeed;
}
// Set angle to direction
image_angle = direction;
// Set speed
x = x + (dcos(direction) * velocity);
y = y - (dsin(direction) * velocity);
// Vector angle between homing missile and target
pointDifference = point_direction(x, y, target.x, target.y);
The first thing we call is the built in GMS2 function called point_direction(). This function will return the angle we need the homing missile to be so that the head of the homing missile points at the main player. We store the result in the variable pointDifference.
// Sin in degrees of vector angle minus current direction
angleDirection = dsin(pointDifference - direction);
So the variable angleDirection is the subtraction of the pointDifference and the current direction (built in GMS2 variable) of the homing missile, and then that value is inside of the built in GMS2 function dsin(). Using dsin() isn’t necessary but it makes our lives easier, because we now only need two conditional if statements to determine which direction the homing missile needs to turn to point at the main player. (If we didn’t use dsin() then we would need to check if pointDiffernce - direction was positive or negative AND if the absolute value of it was > 180 or not.)
// Determine which direction to turn and set direction
if(angleDirection > 0)
{
direction = direction + turnSpeed;
}
else if(angleDirection < 0)
{
direction = direction - turnSpeed;
}
Next we need to know which direction the homing missile needs to rotate (clockwise vs counterclockwise) in order to point at the main player. Now if the angleDirection is positive then we need to add turnSpeed to the current direction (counterclockwise), and if angleDirection is negative then we need to subtract turnSpeed to the current direction (clockwise).
// Set angle to direction
image_angle = direction;
Now we need to set the rotation of the homing missile with image_angle (built in GMS2 variable) which is equal to the newly updated direction. Recall that the variable direction having 0 degrees means the homing missile is pointing to the right, 90 degrees is pointing up, 180 degrees is pointing left, and 270 degrees is pointing down.
// Set speed
x = x + (dcos(direction) * velocity);
y = y - (dsin(direction) * velocity);
Finally we need to have the homing missile move in the direction of the variable direction (that sounds weird lol)! So remember we just calculated the new direction the homing missile will be moving in, which can be 0 to 360 degrees. For example, let’s say the new direction of the homing missile is 45 degrees.
In the image above, the blue line is pointing at 45 degrees, and the orange point is indicating where on the circle the 45 degrees touches. We want the homing missile to move in the same direction as the blue line! You can see there is a triangle with an x and y which we can calculate using basic trigonometry.
x = cos(45 degrees) = ~0.707 and y = sin(45 degrees) = ~0.707
If we move the homing missile with those values (x = x + 0.707, and y = y + 0.707), then the homing missile will move at 45 degrees! But we want to give that movement a speed so we multiple the 0.707 by the velocity (x = x + (0.707 * velocity), and y = y + (0.707 * velocity)).
Looking at the code in the step function, you might be thinking why is the y position MINUS dsin(direction)*velocity?! It is minus because in GMS2, positive is downwards and negative is upwards.
Here is an example image of when direction is 150 degrees:
Here you can see the y value is positive like before, but the x value is now negative.
STEP 3: PLAYING WITH THE INITIAL CONDITIONS
There are two variables for you to play around with:
velocity
turnSpeed
The velocity will determine how fast the homing missile moves, and the turnSpeed will determine how fast the homing missile rotates.
Feel free to leave a comment if there is a programming tutorial you’d like me to do!
I hope y’all enjoyed this homing missile tutorial!